Hi, Im just a newbie here and im trying to program a low pass filter on c# with .wav files. After looking online ive spotted some math formula for RC analogue low pass filters and these formulas i believe are based on voltage. My question is, before the audio is sent to any filter in analogue hardware how would say, a -1->0->1 waveform be sent as a voltage to said filter? Thank you.
How audio is transferred through wiring.
- Thread starter Kevin Cockburn
- Start date
-
- Tags
- analogue low pass filter
Kevin,
An analog RC filter consists of a resistor (R) and a capacitor (C), the relationship between the two values determines the cutoff frequency. You don't "program" analog filters, the formulas determine the physical component hardware needed for the particular filter.
The volume, or amplitude of an analog signal is measured in voltage.
Before any digital audio is sent to any analog hardware, it must be converted to an analog signal, using an D/A (digital to analog) converter.
An analog RC filter consists of a resistor (R) and a capacitor (C), the relationship between the two values determines the cutoff frequency. You don't "program" analog filters, the formulas determine the physical component hardware needed for the particular filter.
The volume, or amplitude of an analog signal is measured in voltage.
Before any digital audio is sent to any analog hardware, it must be converted to an analog signal, using an D/A (digital to analog) converter.
Last edited:
Thank you Art. Ok, so the audio inside the analogue hardware is measured in voltage that makes sense. However because audio fluctuates between two limits(at a given amplitude) what are those values at base levels?(without amplification). Im assuming there is no such thing as a negative voltage, though i'm a layman on the subject.
Not sure what you mean by "base level", analog audio signals are alternating current that vary in positive ("+") and negative ("-") voltage referenced to zero voltage.
The decibel volt reference voltage of 0dBu is +/- 1V RMS (root mean square) .
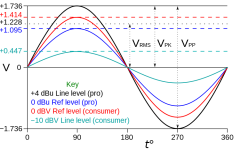
You may find these links useful to expand your understanding:
Line level - Wikipedia
Digital audio - Wikipedia
Audio Signal Filtering - Rhea
Project Rhea: learning by teaching! A Purdue University online education project.
What exactly are you trying to do? You mentioned a C sharp filter? You actually want a filter that will reduce or eliminate just one note, leaving C and D intact?
You've got a little caught up in the clever stuff but have missed quite a bit out.
An audio waveform is an AC voltage, that swings above and below 0 Volts - so it goes positive and negative. With music, this is happening so fast that you can't really imagine it as a sine wave, for example, more like a few thousand or more sine waves all doing different things at the same time. Audio has two components Volume, as in how far away from 0 it goes. In a speaker circuit, it might easily be 70 or 80V peak to peak (as in highest positive going and highest negative going) It could also me a voltage measure in thousandths of a Volt - as in what might come out of a microphone. The other component is pitch - as in the frequency - so somewhere typically between 20 and 20,000Hz.
As said above, to make a filter - a device that reduces voltage at a specific frequency - you need capacitance and inductance. Filters have a 'quality' measured by how much attenuation they can manage, measured in dBs. If you plotted the attenuation against frequency, you could make a filter that removed 10dB at say 5000Hz. At 4500 and 5500Hz, it might only remove 7dB and at 4000 and 6000Hz maybe only 4 dB. So on a piano keyboard and you play C sharp, it would be very quiet. Play the C sharp an octave below and its normal volume. You might find that until you get to say, A, you can't hear a drop on volume. Bb would be quieter, B more quiet, same with C and then C sharp is quietest, then it starts to get louder again. If you increase the 'quality' of the filter, it gets narrower - so a filter has a frequency, an attenuation (or boost) amount and a Q adjustment - the narrowness (quality) of the filter. Simple filters can be very simple - 3 or 4 components, bit the Q of a circuit this simple will mean it's quite wide. Better filters mean they're more complex and clever.
You've got a little caught up in the clever stuff but have missed quite a bit out.
An audio waveform is an AC voltage, that swings above and below 0 Volts - so it goes positive and negative. With music, this is happening so fast that you can't really imagine it as a sine wave, for example, more like a few thousand or more sine waves all doing different things at the same time. Audio has two components Volume, as in how far away from 0 it goes. In a speaker circuit, it might easily be 70 or 80V peak to peak (as in highest positive going and highest negative going) It could also me a voltage measure in thousandths of a Volt - as in what might come out of a microphone. The other component is pitch - as in the frequency - so somewhere typically between 20 and 20,000Hz.
As said above, to make a filter - a device that reduces voltage at a specific frequency - you need capacitance and inductance. Filters have a 'quality' measured by how much attenuation they can manage, measured in dBs. If you plotted the attenuation against frequency, you could make a filter that removed 10dB at say 5000Hz. At 4500 and 5500Hz, it might only remove 7dB and at 4000 and 6000Hz maybe only 4 dB. So on a piano keyboard and you play C sharp, it would be very quiet. Play the C sharp an octave below and its normal volume. You might find that until you get to say, A, you can't hear a drop on volume. Bb would be quieter, B more quiet, same with C and then C sharp is quietest, then it starts to get louder again. If you increase the 'quality' of the filter, it gets narrower - so a filter has a frequency, an attenuation (or boost) amount and a Q adjustment - the narrowness (quality) of the filter. Simple filters can be very simple - 3 or 4 components, bit the Q of a circuit this simple will mean it's quite wide. Better filters mean they're more complex and clever.
Thank you for your response. The c# i meant(but sadly ommited) is the programming language, not the actual note(although its quite a comical crossing of wires
) I wasnt aware of such thing as negative voltage. I think thats the biggest wow moment for me. In memory on computer sounds are discreet samples measuring between 1 and -1 and i was unaware how to convert that into voltage...i was overcomplicating things, but minus voltage actually makes this a lot simpler to convert. So now i have to study up on decibels and then ill be able to plug these formulae in and hopefully get a result close to actual low pass filter outputs. Although it may be a bit more difficult because low pass filtering a 1v waveform will probably produce a different result if low pass filtering say a 40v waveform. That would require dealing with these samples outside their +/-1 limits. One way would be always to normalise the sound which i think is how a digital low pass filter would work anyway...
Sorry - I'm totally lost now. Are you making filters for audio circuits? Low cut is a frequent demand on audio, but low pass is not really something I've ever done - well, for practical music - I've clearly done it to remove the treble and leave the bass, but I don't think this is what you're trying to do. I also don;t get this 1 and -1 sample measurement? What uses 1/-1 levels. Computers tend never to go above 5v do they? That's the supply rail voltage.
You're only going to get a 40V peak to peak waveform in a speaker circuit, and there's not just 40V, but serious current too?
This makes me think we're talking about totally different things. What exactly are you trying to low pass?
You're only going to get a 40V peak to peak waveform in a speaker circuit, and there's not just 40V, but serious current too?
This makes me think we're talking about totally different things. What exactly are you trying to low pass?
Hi, sorry for the confusion. The -1 to 1 value is how the audio is stored in digital memory. Eg, cd audio is 16 bit, so there are 65536 representations per sample represented as 1/65536 steps). This is the audio i want to low pass filter but now im becoming aware that i need to have my program express this audio in an analogue fashion to decipher the db. (This -1 to 1 range is whats seen when you look at a waveform visually, and is the audio at its most basic form before amplifiers or any filters have been applied.) So this sample of audio is stationary and is fed to the filters to create the change. Im still a bit wooly as to how db works and how it is associated with this basic sample representation. And also i am unaware how to have the analogue version of the sample be created so that it can be fed into the (emulated) filters in the first place. Assume i have only digital representation and only my own software to do the legwork...Hope thats a little clearer.
I'm still very confused, I'm afraid. How is this strange -1/+1 stream created? Surely it has to go back to 0/5V to be processed? I really can't help as the filters you're talking about are something I have never looked into. I always thought the filter was to remove the harmonics of the square waves created? I probably misunderstood years ago and never put myself right.
Yes, it will be converted to voltage at some point in the pipeline to actually hear it out speakers but it cant just be stored as voltage, but rather digitally. Like th audio is stored on usb or hd or on cd or in computer ram and it has a format in binary. The 1 and -1 represent the air pressure of the mic recording. This happens 44100 times a second per channel(2 on cd). Every one of those samples is between 1 and -1, 0 would be total silence, ie no air pressure. If your not really computer knowledgable i understand its a bit wierd. Almost as wierd as analogue circuitry is to me 
No, the captured sampled digital waveform is always positive. I'm OK with computers, but the maths element of sampling is usually actioned with an offset, so say a -.5 to +.5 voltage swing has to be converted to a 0 to 1V version to be sampled in the usual manner. This conversion is the aspect I am confused by because of the requirement to know the 'swing'. A small waveform or a big waveform would need to be altered in offset to move the central (old) 0V crossover to half of the maximum voltage swing, so in a 5V TTL type circuit, the crosspoint would be at 2.5V. I don't understand exactly how a conventional AC waveform can be made 100% so it can be sampled. This is required because each digital word in the sampling system needs to swing from digital 0 to digital max, at whatever bit rate you are sampling at. I'm happy with Nyquists work, but I have never understood how the conversion from AC to DC actually works. I completely understand the concept of the analogue waveform, but am stuck at the conversion to the digital levels individually recorded in the sequence. How do they get actually sampled at an accurate point in time, as a positive value. Or does the digital sampling split negative and positive halves and somehow amalgamate them in the sample result?
Ok. So a cd sample is 44100hz and 16 bit. The sample polarities are between -1 to 1. I think it just polls the mic at these intervals to get the air pressure in analogue before changing it to digital though im completely ignorant of that process. The way your describing it in analogue form -1v to 1v seems to be whats happening and if so that would make the conversion relatively easy as its a unit to unit match...(or is it -5 to 5v)? Either way thats a linear exchange which if true is very helpful. In digital if i have multiple samples if add them together the resulting waveform can be above 1 and below minus1 but you can normalise this sample(ie go through every sample and find the most extreme peak in either direction) and then just multiply every sample by this value to squeeze it back to 1>-1. If you were to play a sample that goes out of these boundaries youd hear a horrible distortion where it goes above them as it just turns every sample that goes above to 1 and every sample that goes below to -1.
16bit sample is 65536 possible combinations.
0 is neutral
32767 is 1
-32768 is minus 1
And all the inbetween states away from zero in either direction are the steps(converted into floating point numbers)
65536 combinations can be represented as either 0->65535 or -32768->32767 depending on whats required from the user for a 16bit value.
So as far as the computer is concerned it always fires samples to the analogue hardware in this fashion and its up to the amplifier to magnify the voltage for volume. (I think you said +-40v). Im trying to do my low pass filter(and any other filter) before sending it to the player(which i suppose you could connect a mixer to this output to get the correct results) but wheres the fun in that?
16bit sample is 65536 possible combinations.
0 is neutral
32767 is 1
-32768 is minus 1
And all the inbetween states away from zero in either direction are the steps(converted into floating point numbers)
65536 combinations can be represented as either 0->65535 or -32768->32767 depending on whats required from the user for a 16bit value.
So as far as the computer is concerned it always fires samples to the analogue hardware in this fashion and its up to the amplifier to magnify the voltage for volume. (I think you said +-40v). Im trying to do my low pass filter(and any other filter) before sending it to the player(which i suppose you could connect a mixer to this output to get the correct results) but wheres the fun in that?
What are you going to achieve with filtering the analogue output - that's not what digital filters do? You seem to have a basic grasp, but your analogies are a bit odd. Sound pressure is an analogue function between a source and a transducer. If a sample goes out of the range you do NOT hear a nasty distortion, it will depend on how long that distortion is maintained. You can have many thousand errors every second corrected - basically looking at the waveform and using an algorithm to put back in a sample value that is best guess. You can record an audio stream that sounds great and then when you look in an editor see huge spikes up to maximum that are very short, and totally missed. You can see errors in the data stream so that the point where the negative waveform crosses the line and goes positive gets shifted and again, these errors are often invisible to then ear. This idea of -1 and 1 sample polarities is also a red herring. Your input voltage could be .775V or 1.4V - measured as an AC waveform, peak to peak. At some point, the device has to decide what voltage = digital maximum, and of course this is usually made variable - so it's possible to record too low and too high. Full scale levels are always described as bad, because all we really want is the range between 0 and full. what constitutes full we fiddle with between brands and device types. We even get it more confused when we talk about balanced inputs because these swing either side of the 0V crosspoint, but an unbalanced signal also exhibits this swing, but gets measured differently. I've read so many articles on the A-D-A process at GCSE to PhD level that's easy to spot how difficult the entire concept is, because the basic function of chopping up, recording the level and reconstituting is quite simple - the problems come from the noise created by the stepped waveform that creates harmonics that need removing with usually filters. That's when it gets tricky!